
Curvas e sua arte
Curvas rolantes
A ideia de curva que possuímos hoje não é a mesma que os gregos tinham, por exemplo. A geometria grega foi desenvolvida inicialmente a partir de uma série de problemas cujos resultados eram obtidos, geralmente, utilizando instrumentos capazes de construir geometricamente a soma, subtração, produto, divisão, assim como a raiz quadrada. Entretanto, no século V a.C, os gregos se deparam com alguns problemas que não poderiam ser resolvidos com tais instrumentos. Estes problemas são conhecidos como os três problemas clássicos gregos.

Os três problemas clássicos da geometria são: a trissecção de um ângulo, a quadratura do círculo e a duplicação do cubo.
Séculos depois, por volta do ano de 1882, demonstrou-se que estes três problemas eram impossíveis de serem resolvidos utilizando apenas aqueles instrumentos. Para resolvê-los, criaram-se algumas curvas, que poderiam ser construídas com régua e compasso e sua construção era realizada a partir da combinação de movimentos no plano. Os gregos as denominaram de curvas mecânicas, que também são conhecidas como curvas rolantes ou curvas cíclicas.
De modo geral, as curvas rolantes são curvas planas, geradas por um ponto pertencente a uma circunferência que roda, sem deslizar, sobre outra circunferência ou uma reta.
1.

Vamos desenhar algumas dessas curvas?! Para isso, vamos utilizar um aplicativo chamado Geogebra (ggbm.at/ERyjESxV). Movimente o seletor t para ver a animação.

Para descobrir o nome da curva que criamos, resolva o criptograma a seguir. O nome da curva será formado pelas letras nas casinhas verdes.
2. Criptograma
- As casinhas com o mesmo símbolo têm a mesma letra;
- Complete somente as palavras que tem certeza;
- Letras com e sem acentuação são iguais para o jogo, isto é: Á = A, C = Ç, Ã = A, etc.
| Capital do Estado de Pernambuco | ||||||
| Pagar, Saldar | ||||||
| Que se socou | ||||||
| Que contém sal | ||||||
| Espécie de Pincel | ||||||
| Habitante de Goiás | ||||||
| Capital da Espanha | ||||||
| Mergulhado, submerso |

Agora que já conhecemos o nome desta curva, vamos defini-la:
Chama-se uma curva plana descrita por um ponto de uma circunferência que rola, sem deslizamento, sobre uma reta. Esse ponto é chamado de gerador, a circunferência de geradora e a reta de diretriz da .
3. Qual a equação?

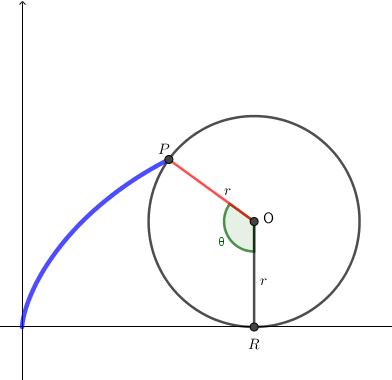
Desafio você a encontrar as equações paramétricas da cicloide. Para isso, considere um círculo de centro $O$ e raio $r$, uma reta $s$ e um ponto $P$ no círculo. Faça o círculo deslizar e encontre a parametrização da curva em relação ao raio e ao ângulo $\theta$. Use os botões para facilitar a inserção de alguns símbolos matemáticos.
Escreva aqui a equação. Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, utilize os botões para lhe auxiliar.
$x = $
$y = $
4. Abstração geométrica com a cicloide

Que tal fazermos arte com a cicloide?! Quero que você conheça o pintor brasileiro Hermelindo Fiaminghi. Ele nasceu em São Paulo e dedicou-se a abstração geométrica. Veja algumas obras dele neste site: bit.ly/2JUDh4E.

|

|
Fonte: bit.ly/2Hbv8XU
Inspirando-se em uma das obras Hermelindo Fiaminghi, use a cicloide para fazer uma bela releitura.

Lembre-se: releitura é uma nova interpretação de uma obra de arte, feita com estilo próprio, mas sem fugir ao tema original da obra.
