
Fractais e sua arte
Árvore Bifurcada

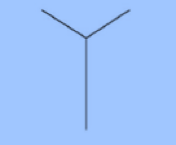
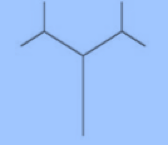
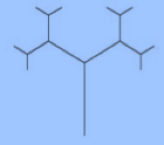
Para construírmos o fractal árvore bifurcada consideramos como gerador um segmento de comprimento $L$ (vamos tomar $L=1$) e os seguintes passos:
- Reduzimos o segmento à metade;
- Inserimos dois segmentos de forma bifurcada junto a extremidade superior do segmento inicial, com ângulo de bifurcação de 120º e com o tamanho obtido na redução do nível anterior;
- Repetimos, indefinidamente, este processo em cada um dos novos segmentos.
 |
 |
 |
 |
26.
Complete corretamente a tabela com os resultados obtidos na n-ésima iteração do processo de construção da Árvore Bifurcada:
| Etapas | $$0$$ | $$1$$ | $$2$$ | $$3$$ | ... | $$n$$ |
| Número de segmentos | $$1$$ | $$2$$ | $$2^{2}$$ | $$2^{3}$$ | ... | |
| Comprimento de cada segmento | $$1$$ | $$\Big(\frac{1}{2}\Big)$$ | $$\Big(\frac{1}{2}\Big)^2$$ | $$\Big(\frac{1}{2}\Big)^3$$ | ... | |
| Comprimento total | $$1$$ | $$2$$ | $$3$$ | $$4$$ | ... |
Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.

No vídeo (youtu.be/yWRFCSIzej0) temos uma bela animação da Árvore Bifurcada.
Abaixo apresentamos várias árvores bifurcadas com fator de redução 1,5 e sete iterações:
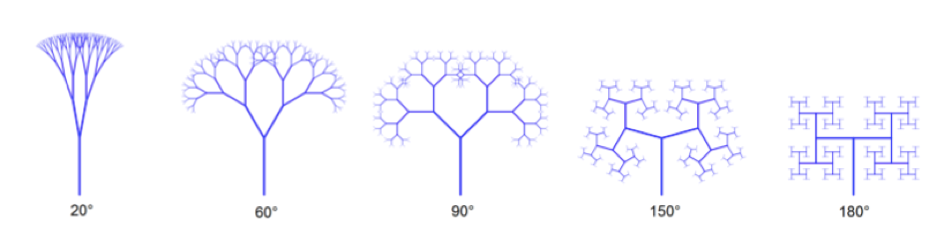

No site: bit.ly/2H8C5g9 você encontrará um gerador de árvores fractais. Divirta-se!
See the Pen Fractal Tree Generator by Andrew Herman (@hippiefuturist) on CodePen.
27.

Qual a dimensão fractal da Árvore Bifurcada?
Para construirmos a árvore bifurcada do seguite modo: dado um segmento unitário como gerador:
- Reduzimos a metade este segmento e giramos, no sentido anti-horário, por um ângulo theta;
- Reduzimos a metade este segmento e giramos, no sentido horário, por um ângulo theta;
- Aplicamos a função identidade para manter os ramos nas posições desejadas.
Como a terceira função não é uma contração, não podemos aplicar a fórmula da dimensão por autossimilaridade. Podemos mostrar que existe um fator crítico $r_{c}$ tal que a árvore bifurcada é autossimilar. Podemos mostrar que, para $theta = 60º$ temos que $r = 0.58$. Então, para este caso, $m = 2$ e $r = 0.58$ e $d =$
28.
Uma das figuras abaixo não tem nenhuma imagem de fractais. Qual é?
