Fractais e sua arte

Árvore Pitagórica

O fractal Árvore Pitagórica é um fractal construído usando-se a interpretação geométrica do Teorema de Pitágoras. Seguindo os passos abaixo, você aprenderá como construir este fractal.

Construa um quadrado;
Usando como base o lado de cima (topo) deste quadrado, construa um triângulo retângulo tendo como hipotenusa a base;
Em seguida, nos dois catetos restantes do triângulo, construa dois novos quadrados cujos lados são exatamente os catetos;
Repita os três passos anteriores nos dois novos quadrados.

Instrução: clique nas formas pontilhadas abaixo para construí-las.

Repita os três primeiros passos nos novos quadrados indefinidamente.

Veja no vídeo (youtu.be/xiXZAas5Rc4) algumas etapas do processo iterativo da construção da Árvore Pitagórica

22.

Marque a alternativa que completa corretamente os resultados obtidos na n-ésima iteração do processo de construção da Árvore Pitagórica:

Etapas	$$0$$	$$1$$	$$2$$	$$3$$	...	$$n$$
Número de triângulos	$$1$$	$$2^{1}$$	$$2^{2}$$	$$2^{3}$$	...

(a) $2^{n-1}$

(b) $2^{n}$

(d) $2^{n-2}$

Número de Quadrados

$$2$$

$$2^{2}$$

$$2^{3}$$

$$2^{4}$$

...

(a) $2^{2n}$

(b) $2^{n}$

(d) $2^{n+1}$

23.

Vamos numerar nossa Árvore Pitagórica do seguinte modo: o quadrado inicial será o número $1$. Para o nível $n$, os quadrados da esquerda são $2n$ e os da direita $2n+1$. Complete a numeração dos quadrados da Árvore Pitagórica subsituindo as letras pela numeração correta:

(A):

(B):

(C):

(D):

(E):

(F):

(G):

(H):

(I):

(J):

(K):

(L):

(M):

(N):

(O):

(P):

(Q):

(R):

(S):

(T):

(U):

(V):

(X):

(W):

(Y):

(Z):

(AA):

(AB):

24.

DesaPhio e o seu cão guia, Phiel, explicando algo

Inventei um código para localizar um quadrado na Árvore Pitagórica que acabamos de numerar.

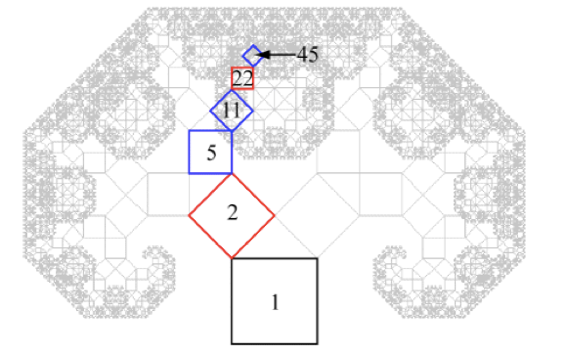
Este código usa a base binária. Por exemplo, quero localizar o quadrado 45, como $45=32+8+4+1$ então tem representação 101101 na base binária. Meu código é o seguinte: o primeiro dígito representa o quadrado inicial, para os dígitos seguintes, um zero significa virar para a esquerda e o 1 significa virar para a direita. Então, para chegar ao quadrado 45, vá para a esquerda, direita, direita, esquerda, direita. Isso está ilustrado na figura abaixo:

Árvore pitagórica com destaque nos quadrados 1, 2, 5, 11, 22, 45

Fonte: bit.ly/2rsZxee

Usando este código localize o quadrado 116 na Árvore Pitagóriga abaixo:

Dica: $116 = 64+32+16+4$

25.

a) Descubra o nome da curva formada quando unimos os pontos verdes dos quadrados 2, 4, 8, 16, 32, 64, 128 da Árvore Pitagórica.

A curva chama-se .

b) Indique na árvore abaixo outros quadrados que unindo-se pontos podemos formar a curva do item (a).

Podemos construir a Árvore Pitagórica usando qualquer imagem, como mostra a seguinte figura:

Árvore pitagórica com a cabeça da Phiphi se repetindo dentro dos quadrados

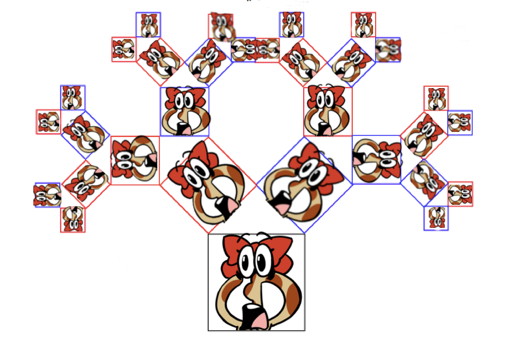
Vamos fazer um porta-retrato de Árvore Pitagórica. Insira uma imagem e ela será inserida em cada quadrado da árvore abaixo:

Use o aplicativo Mosaico Fractal (editaedi.ufpa.br/ferramentas/mosaico) para criar uma obra usando a Árvore Pitágorica. A imagem abaixo foi criada pela profa. Cristina Vaz.

Bolinhas rosas preenchendo uma árvore pitagórica roxa