Fractais e sua arte

Dimensão fractal & Natureza

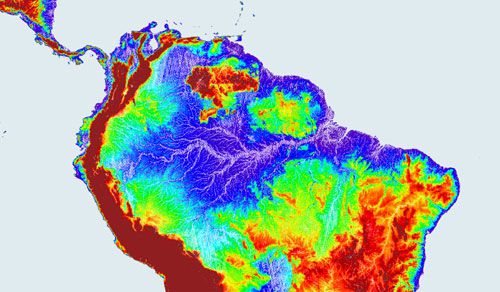
A geometria fractal é muito usada para modelar objetos que aparecem na Natureza tais como rios, relâmpagos e árvores. Muitos destes modelos fractais não são autossimilares ou são estatisticamente autossimilares ou são gerados por um processo caótico. Seguem alguns exemplos (fonte: bit.ly/2qGRObj):

A dimensão fractal do sistema fluvial do rio Amazonas é 1.85.

A dimensão fractal dos relâmpagos é 1.51.

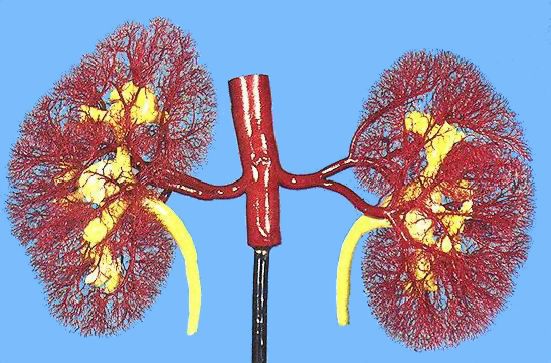
A dimensão fractal dos angiograms dos rins é 1.61.

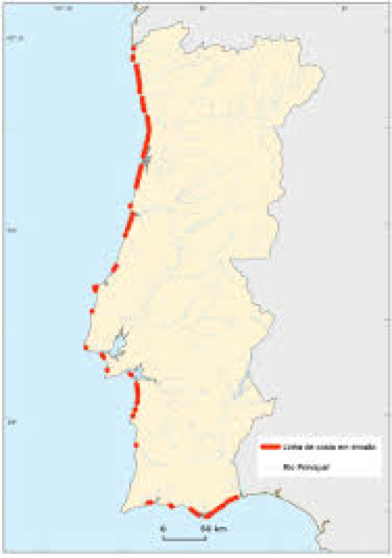
A dimensão fractal da costa de Portugal é 1.41.

Phida ao lado da obra de Pollock, chamada Number 32

Fonte: bit.ly/2H91pD1

"Qual será a dimensão fractal desta obra de Pollock?"

Para calcularmos uma aproximação da dimensão por contagem de caixas destes fractais cobrimos a imagem com uma malha e contamos o número de caixa que contém partes da imagem. Repetimos o processo com malhas cada vez menores.

Da definição da dimensão por contagem de caixa temos que a lei de potência $N(r) \cong C/r^{d}$ pode ser usada para este cálculo. Portanto

$$\ln (N(r)) = d \ln (1/r) +\ln (C)$$ Se usarmos malhas de comprimento $r_{1}, r_{2}, ..., r_{n}$ temos que $d$ é a inclinação da reta que melhor se ajusta aos seguintes pontos:

$$x_{i}$$	$$y_{i}$$
$$\ln (1/r_{1})$$	$$\ln (N(r_{1}))$$
$$\ln (1/r_{2})$$	$$\ln (N(r_{2}))$$
$$\ln (1/r_{3})$$	$$\ln (N(r_{3}))$$
...	...
$$\ln (1/r_{n})$$	$$\ln (N(r_{n}))$$

Phida ao lado da obra de Pollock, chamada Blue Poles

Fonte: bit.ly/2vqwIn5

"Usando esta técnica, Taylor mostrou que a dimensão fractal do quadro Blue Poles é 1,72." - Fonte: bit.ly/2JSrcwN

REFERÊNCIAS
TAYLOR, Richard P. Order in Pollock’s chaos. Scientific American, v. 287, n. 6, p. 116-121, 2002. (link: bit.ly/2JSrcwN)