Fractais e sua arte

 Os fractais possuem uma proriedade muito interessante chamada autossimilaridade. A autossimilaridade é uma ideia antiga e uma propriedade geométrica simples. É a "simetria através das escalas", ou seja, um objeto possui autossemelhança se apresenta a mesma forma em qualquer escala em que seja observado. Naturalmente, nem todos os objetos geométricos têm esta propriedade. Por exemplo, um círculo numa escala muito grande não é nada mais do que uma reta.

 Por outro lado, um quadrado é um conjunto autossimilar do plano, pois pode ser formado por quatro cópias deles mesmo reduzidas por um fator $k$. Matematicamente, a propriedade de autossimilaridade é descrita por transformações cujas imagens dos objetos sejam "cópias reduzidas" do mesmo. Tais transformações são chamadas transformações similares.

 Podemos construir um objeto autossimilar reduzindo (ou ampliando), rodando e/ou transladando este objeto. Por exemplo, considere um quadrado $Q$ unitário com um dos vértices na origem, se queremos reduzir este quadrado à metade (fator de redução $\frac{1}{2}$) devemos “transformar'” todos os pontos deste quadrado em novos pontos cujas coordenadas serão a metade das coordenadas dos pontos originais, como mostra a seguinte figura:

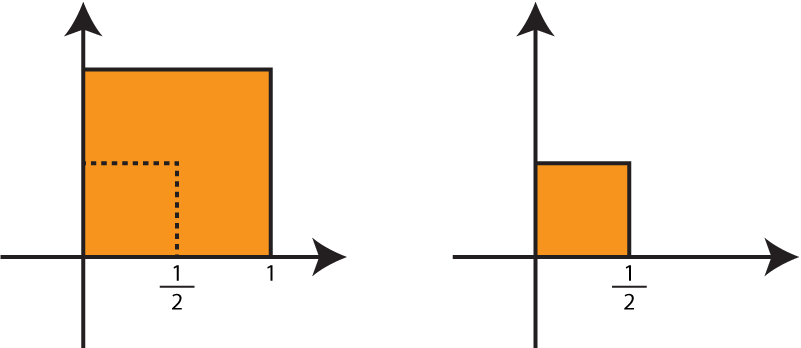
 Matematicamente, este processo é descrito do seguinte modo: se $P=(x,y)$ é um ponto de $Q$ com coordenadas $(x,y)$, para reduzirmos os pontos de $Q$ à metade transformaremos $P=(x,y)$ no ponto $P_{1}=(x_{1},y_{1})$ com coordenadas $x_{1}=\frac{x}{2}$ e $y_{1}=\frac{y}{2}$. Representamos esta transformação na forma: $f_{1}=(x,y)$ $=(\frac{x}{2},$ $\frac{y}{2})$.

 O mesmo vale para translação, para rotação e composições destas transformações.

 Por exemplo, se queremos transladar $Q$ duas unidades à direita da sua posição inicial devemos "transformar" todos os pontos de $Q$ em novos pontos cujas coordenadas serão as coordenadas originais mais duas unidades. Logo, transformaremos o ponto $P=(x,y)$ no ponto $P_{1}$ $=(x_{2},y_{2})$ com coordenadas $x_{2}=x+2$ e $y_{2}=y$. Repesentamos esta transformação na forma: $f_{2}(x,y)$ $=(x+2,y)$.

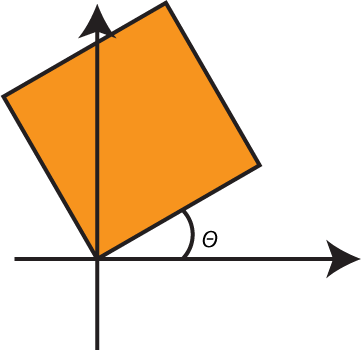
 Agora, se quisermos rodar $Q$ por um ângulo $\thetaº$ no sentido anti-horário, cada ponto $P=(x,y)$ de $Q$ deve ser transformado no ponto $P_{3}=$ $(x_{3},y_{3})$ de modo que $x_{3} = x \cos(\theta)$ $– y \textrm{ sen}(\theta)$ e $y_{3} = x \textrm{ sen}(\theta) + y \cos(\theta)$ (Veja a figura abaixo. Repesentamos esta transformação na forma: $f_{3}(x,y)=(x$ $\cos(\theta)$ $– x \textrm{ sen}(\theta)$ $+ y \cos(\theta))$.

---

12.

 Considerando que a cor branca significa ausência:

(a) Quantas cópias similares da figura

você vê na figura abaixo?

(b) Quantas cópias similares da figura

você vê na figura abaixo?

(c) Quantas cópias similares da figura

você vê na figura abaixo?

(d) Quantas cópias similares da figura

você vê na figura abaixo?

---

13.

 Para descrevermos o processo iterativo do Triângulo de Sierpinski precisamos de três transformações. As duas primeiras transformações são

$f_{1}(x,y)$=$\Big(\frac{x}{2},\frac{y}{2}\Big)$ $\textrm{ e } f_{3}(x,y)$=$\Big(\frac{x}{2}$ $+\frac{1}{4}, \frac{y}{2}$ $+\frac{\sqrt{3}}{4}\Big).$

(a) Qual a segunda transformação?

$f_{2} (x,y)=$

  Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.

 Ao aplicarmos as transformações similares $f_{1}(x,y)$, $f_{2}(x,y)$ e $f_{3}(x,y)$ no triângulo equilátero inicial, vamos gerar uma sequência de figuras $S_{n}$, $n \in N$. Por exemplo, para $n=6$ temos a seguinte sequência:

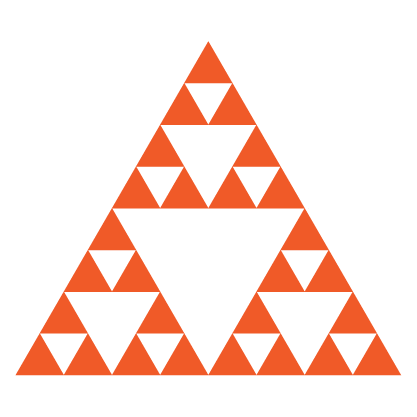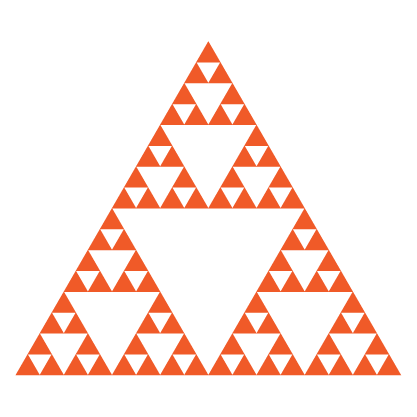$$S_{1}$$	$$S_{2}$$	$$S_{3}$$	$$S_{4}$$	$$S_{5}$$	$$S_{6}$$

 Note que cada figura da sequência acima é formada por três cópias reduzidas da figura anterior e $3^{n}$ cópias do gerador. Por exemplo, a figura $S_{3} = f_{1}$ $(S_{2}) \cup f_{2}$ $(S_{2})$ $\cup f_{3} (S_{2})$.  Portanto, se $S_{n}$ é a figura gerada no n-ésimo passo temos que

$S_{3} = f_{1}$ $(S_{2}) \cup f_{2}$ $(S_{2}) \cup f_{3}$ $(S_{2}).$

---

(b) Para descrevermos o processo iterativo do Tapete de Sierpinski precisamos de oito transformações. Quais são as quatro primeiras transformações?

$f_{1} (x,y)=$

$f_{2} (x,y)=$

$f_{3} (x,y)=$

$f_{4} (x,y)=$

  Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.

 Ao aplicarmos as transformações similares $f_{1}(x,y)$, $f_{2}(x,y)$, $f_{3}(x,y)$, ..., $f_{8}(x,y)$ no quadrado inicial, vamos gerar uma sequência de figuras $Q_{n}$, $n \in N$. Por exemplo, para $n=4$ temos a seguinte sequência:

$$Q_{1}$$	$$Q_{2}$$	$$Q_{3}$$	$$Q_{4}$$

 Note que cada figura da figura acima é formada por oito cópias reduzidas da figura anterior e $8^{n}$ cópias do gerador. Por exemplo, a figura $Q_{3}$ é dada por

$Q_{3} = f_{1}$ $(Q_{2}) \cup f_{Q}$ $(Q_{2}) \cup f_{3}$ $(Q_{2})$ ... $\cup f_{8} (Q_{2}).$

 Portanto, se $Q_{n}$ é a figura gerada no n-ésimo passo temos que

$Q_{n} = f_{1}$ $(Q_{n-1}) \cup f_{Q}$ $(Q_{n-1}) \cup f_{3}$ $(Q_{n-1})$ ... $\cup f_{8} (Q_{n-1}).$

---

14.

$f_{1} (x,y)=$

$f_{2} (x,y)=$

$f_{3} (x,y)=$

$f_{4} (x,y)=$

$f_{5} (x,y)=$

  Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.

---

15.

 Indique qual das figuras abaixo representa a imagem do fractal que você criou.

(a)	(b)	(c)	(d)