Fractais e sua arte

	$$r=1$$	$$N(1)=1$$
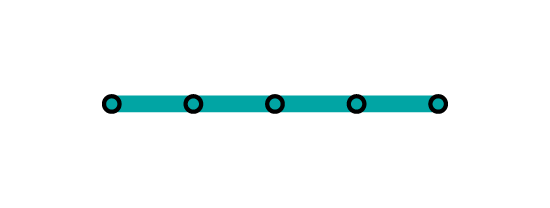
	$$r=\frac{1}{2}$$	$$N\Big(\frac{1}{2}\Big)=2$$
	$$r=\frac{1}{2=4}$$	$$N\Big(\frac{1}{4}\Big)=4$$
	$$r=\frac{1}{8}$$	$$N\Big(\frac{1}{8}\Big)=8$$

 Observe que, neste caso, $N(r)=\frac{1}{r}$.

 Agora, considere $E$ um quadrado unitário e $N(r)$ o número de quadrados de diâmetro (lado) $r > 0$ (caixas) necessários para cobrir $E$. Veja alguns casos:

	$$r=1$$	$$N(1)=1$$
	$$r=\frac{1}{2}$$	$$N\Big(\frac{1}{2}\Big)=4$$
	$$r=\frac{1}{2=4}$$	$$N\Big(\frac{1}{4}\Big)=16$$
	$$r=\frac{1}{8}$$	$$N\Big(\frac{1}{8}\Big)=64$$

 Observe que, neste caso, $N(r)=\Big(\frac{1}{r}\Big)^{2}$.

 Agora, considere $E$ um triângulo retângulo de catetos unitários e $N(r)$ o número de quadrados de diâmetro (lado) $r > 0$ (caixas) necessários para cobrir $E$. Veja alguns casos:

	$$r=1$$	$$N(1)=1$$
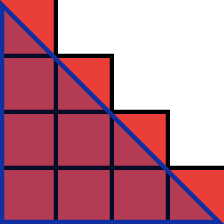
	$$r=\frac{1}{2}$$	$$N\Big(\frac{1}{2}\Big)=3$$
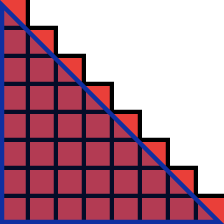
	$$r=\frac{1}{2=4}$$	$$N\Big(\frac{1}{4}\Big)=10$$
	$$r=\frac{1}{8}$$	$$N\Big(\frac{1}{8}\Big)=36$$

 Observe que, neste caso, $N(r)=\frac{r(r+1)}{2}$.

 Estamos interessados na taxa de crescimento de $N(r)$ quando $r \to 0$. Se $E$ é um conjunto finito então $N(r) \cong C$, com $C$ uma constante. Se $E$ é uma curva "regular" então $N(r) \cong C/r$. A ideia principal é que para conjuntos com dimensão n temos que $N(r) \cong C/r^{n}$ com o índice $n$ igual a dimensão topológica de $E$. Portanto, $$n = \frac{\ln(N(r))}{\ln (1/r)}$$  Considerando estas ideias, podemos definir uma dimensão obtida por uma escala r, ou seja, para cada r, medimos o conjunto ignorando as "irregularidades" que podem acontecer em tamanhos menores que r e analisamos como esta medida se comporta quando quando $r \to 0$. Em geral, a dimensão de $E$ é determinada por uma lei de potência satisfeita por $N(r)$ quando $r \to 0$.

 Se $C$ e $d$ são constantes e $N(r) \cong (1/r)^{d}$ podemos dizer que a dimensão de $E$ é $d$. Deste modo, tomando o logaritmo e fazendo $r \to 0$ obtemos $$d = \lim_{r \to 0}\frac{\ln(N(r))}{\ln (1/r)}$$ Esta dimensão é conhecida como dimensão por contagem de caixas.

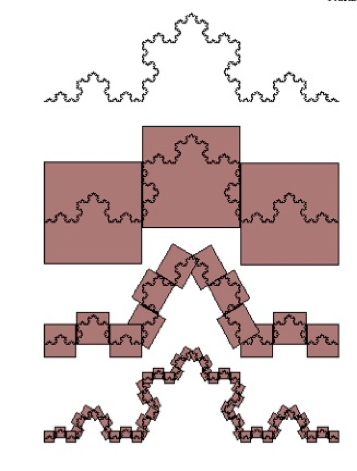	$$N(1/3)=3$$
	$N(1/9)=$ $N((1/3)^{2}) =$ $12 = 3 \times 4$
	$N(1/27)$ $=N((1/3)^{3}) =$ $48 = 3 \times 4^{2}$
	...
	$N((1/n)^{n})$ $= 3 \times$ $4^{n-1}$
	$d=$ $\lim_{x\to\infty} \frac{\log (3 \times 4^{n-1})}{\log 3^{n}}$
	$d=\frac{\ln (4)}{\ln (3)} =$ $1.26$
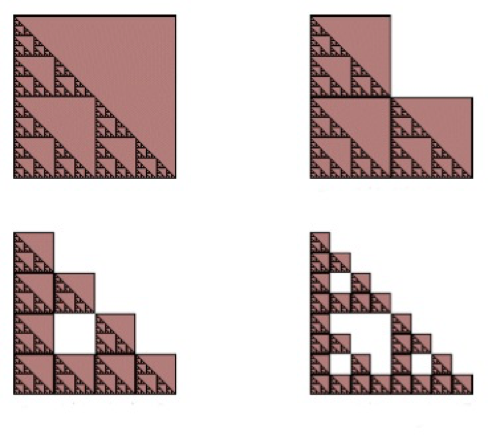	$$N(1)=1$$
	$$N((1/3)) = 8$$
	$N(1/9)=N((1/3)^{2}) =$ $64 = 8^{2}$
	$N(1/27)=N((1/3)^{3}) =$ $256 = 8^{3}$
	...
	$$N((1/n)^{n}) = 8^{n}$$
	$$d=\lim_{x\to\infty} \frac{\log 3^{n}}{\log 2^{n}}$$
	$d=\frac{\ln (3)}{\ln (2)}$ $= 1.58$
	$$N(1)=1$$
	$$N((1/3)) = 8$$
	$N(1/9)=N((1/3)^{2}) =$ $64 = 8^{2}$
	$N(1/27)=N((1/3)^{3}) =$ $256 = 8^{3}$
	...
	$$N((1/n)^{n}) = 8^{n}$$
	$$d=\lim_{x\to\infty} \frac{\log 8^{n}}{\log 2^{n}}$$
	$$d=\frac{\ln (8)}{\ln (2)} = 1.89$$

---

21.

 Calcule a dimensão por contagem de caixa da Esponja de Menger.