Fractais e sua arte

 Um segmento de reta é um objeto autossimilar, pois pode ser formado por quatro segmentos similares:

 Note que, usamos quatro transformações similiares cada uma com fator $\frac{1}{4}$. Agora, considere a seguinte equação:

$\Big(\frac{1}{4}\Big)^{s}$ $+\Big(\frac{1}{4}\Big)^{s}$ $+\Big(\frac{1}{4}\Big)^{s}$ $+\Big(\frac{1}{4}\Big)^{s}$ $=1\textrm{, ou seja, } 4\Big(\frac{1}{4}\Big)^{s}$ $=1.$

 Observe que a solução desta equação é $s=1$.

 Um quadrado é um objeto geométrico autossimilar, pois pode ser formado quatro quadrados similares:

 Note que usamos quatro transformações similares cada uma com fator $\frac{1}{2}$. Considere a seguinte equação:

$\Big(\frac{1}{2}\Big)^{s}$ $+\Big(\frac{1}{2}\Big)^{s}$ $+\Big(\frac{1}{2}\Big)^{s}$ $+\Big(\frac{1}{2}\Big)^{s}$ $=1\textrm{, ou seja, } 4\Big(\frac{1}{2}\Big)^{s}$ $=1.$

 Observe que a solução desta equação é $s=2$.

 Assim, seja $E$ é o atrator do Sistema de Funções Iteradas – IFS, $\{f_{1}, f_{2}, ..., f_{m}\}$ cada uma com fator de similaridade $\{r_{1}, r_{2}, ..., r_{m}\}$. Se $r_{i} < 1$ então existe um único número positivo $s$ tal que $$r_{1}^{s}+r_{2}^{s}+...+r_{m}^{s}=1$$ e $s = 0$ para $m = 1$. O número $s$ é chamado dimensão de similaridade do conjunto $E$ quando $E$ é o atrator com IFS $\{f_{1}, f_{2}, ..., f_{m}\}$ e fatores $\{r_{1}, r_{2}, ..., r_{m}\}$. Representamos $s = dim_{S}E$.

 Se os fatores $r_{i}$ são iguais a $r$ temos que $m\Big(\frac{1}{r}\Big)^{s}=1$, ou seja,

$\Big(\frac{1}{r}\Big)^{r}=\frac{1}{m}$ $\Longrightarrow m =$ $r^{s} \Longrightarrow \ln(m) =$ $\ln(r^{s}) \Longrightarrow s=$ $\frac{\ln(m)}{\ln(r)}$

20.

 Complete a tabela abaixo:

Nome do conjunto	Conjunto	IFS	$$r$$	Fator	$$s=dim_{s}E$$
Segmento		$$m=4$$	$$r=4$$	$$\frac{1}{r}=\frac{1}{4}$$	1
Quadrado		$$m=4$$	$$r=2$$	$$\frac{1}{r}=\frac{1}{2}$$	2
Triângulo		$$m=4$$	$$r=2$$	$$\frac{1}{r}=\frac{1}{2}$$
Cubo		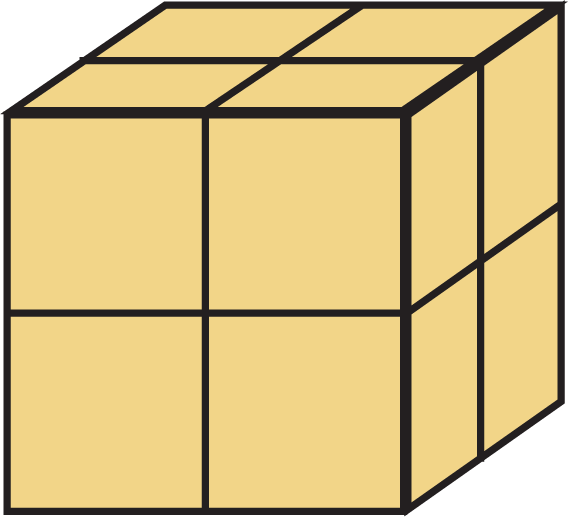$$m=8$$	$$r=2$$	$$\frac{1}{r}=\frac{1}{2}$$
Conjunto de Cantor		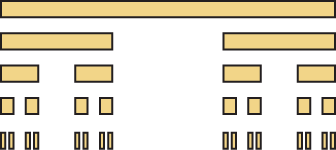$$m=2$$	$$r=3$$	$$\frac{1}{r}=\frac{1}{3}$$
Curva de Koch		$$m=4$$	$$r=3$$	$$\frac{1}{r}=\frac{1}{3}$$
Triângulo de Sierpinski		$$m=3$$	$$r=2$$	$$\frac{1}{r}=\frac{1}{2}$$
Tapete de Sierpinski		$$m=8$$	$$r=3$$	$$\frac{1}{r}=\frac{1}{3}$$
Tapete		$$m=15$$	$$r=4$$	$$\frac{1}{r}=\frac{1}{4}$$
Curva de Hilbert	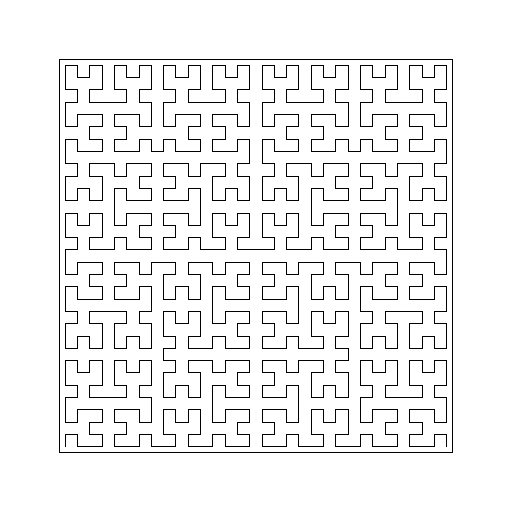Fonte: bit.ly/2IoPZe2	$$m=4$$	$$r=2$$	$$\frac{1}{r}=\frac{1}{2}$$
Esponja de Menger		$$m=20$$	$$r=3$$	$$\frac{1}{r}=\frac{1}{3}$$
Tetraedro de Sierpinski	Fonte: bit.ly/2KNh6Oh	$$m=4$$	$$r=2$$	$$\frac{1}{r}=\frac{1}{2}$$