
Fractais e sua arte
Processo iterativo

Ao longo da história da Matemática, objetos geométricos com características especiais têm desafiado a imaginação e contribuído para o avanço da Matemática. A Curva de Koch, o Triângulo e o Tapete de Sierpinski são alguns exemplos da influência de tais objetos no desenvolvimento da Matemática.
Originalmente construídos como exemplos de conjuntos com propriedades especiais, muito tempo se passou até que sua aplicação fosse percebida pelos matemáticos contemporâneos.

Em 1975, Benoît Mandelbrot, matemático polonês, observou que vários destes conjuntos tinham muitas propriedades comuns e os chamou de Fractais. O termo vem do latim, do adjetivo fractus, derivado do verbo frangere que significa quebrar, fracionar. Entender como estes objetos são gerados é o primeiro passo para aprendermos suas propriedades.
O principal processo para gerarmos fractais é chamado processo iterativo. Iteração significa repetir um processo muitas vezes. Existem vários processos iterativos na Matemática, no caso dos fractais as iterações envolvem uma "regra geométrica".
Inicia-se com algum objeto geométrico chamado gerador. Depois, executa-se uma ou mais operações geométricas no gerador. Esta operação é chamada regra de iteração. A regra de iteração pode envolver rotação, translação, contração no objeto. Ao executarmos a regra de iteração geramos uma nova figura. O próximo passo é fazer uma nova iteração, isto é, executar as mesmas operações nesta nova figura e gerar uma outra figura. Depois repetindo este processo várias vezes, obtemos uma sequência de figuras.
Aplicando-se este processo infinitamente, pergunta-se "qual a figura final que será gerada?" Veremos que iterações geométricas simples podem gerar fractais bem interessantes.
1.
Observe as sequências formadas por Phiphi e complete com o nome das regras de iteração (podem ser aplicada mais de uma regra).
(a)

(b)

(c)

(d)
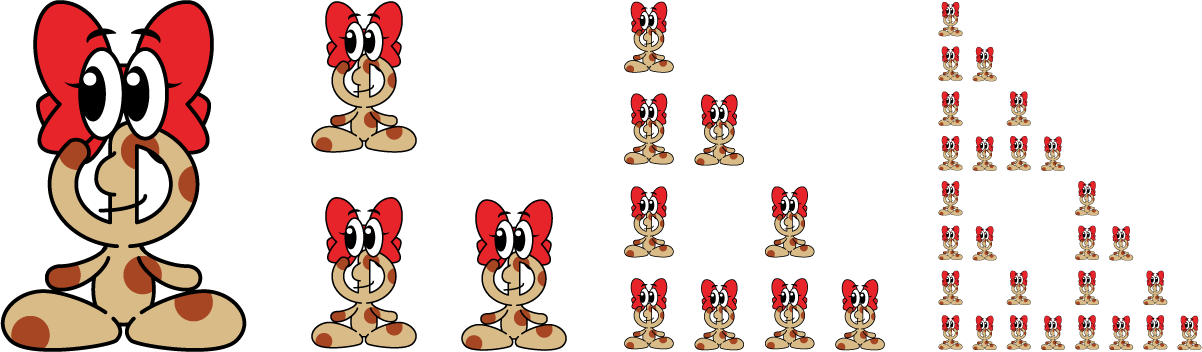
2.

Desafio você a encontrar no caça-palavras a regra de iteração usada no item (a), movendo-se de casa em casa.
| P | R | E | A | R | G | E | B | J |
| N | I | D | O | H | O | R | A | R |
| T | T | G | I | R | L | H | X | I |
| N | N | A | C | O | D | M | H | O |
| R | E | H | V | M | E | A | Z | V |
| L | S | A | I | O | N | O | V | S |
| N | O | J | S | X | A | U | E | N |
| S | U | A | R | G | A | T | N | I |
| Z | A | X | O | E | D | R | E | S |
3.
Substituindo os símbolos pelas letras de acordo com a tabela abaixo descubra os nomes das regras de iteração usadas por Phiphi para formar as figuras do item (d):
| = A | = Ã | = M |
| = C | = Ç | = P |
| = O | = D | = N |
| = U | = L | = S |
| = E | = R | |
| = I | = T |
Regra 1:
Regra 2:
Regra 3:
4.
Se a cor branca significar ausência, quantos triângulos você vê na figura abaixo?

