Fractais e sua arte

 Para construírmos o fractal circular do tipo Dürer (citar a tese do Alceu nas referências) tomemos um círculo qualquer e o subdividimos em seis partes de mesma medida angular. Consideremos a distância de cada uma destas partes até o centro do círculo e a dividamos em 3 partes iguais. Partindo da extremidade exterior, tomemos como novo centro a primeira terça parte e construímos um novo círculo em cada um desses pontos com raio 1/3 do círculo maior, gerando 6 novos círculos e removendo-se o círculo inicial. Depois repetimos o processo em cada um dos novos círculos indefinidamente.

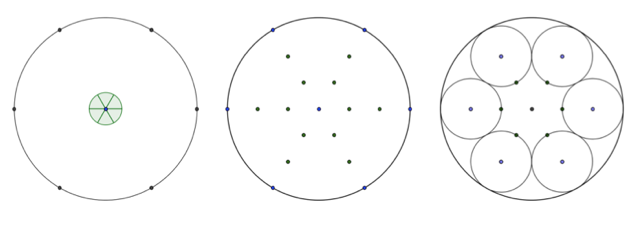
29.

 Vamos desenhar algumas etapas do Fractal circular do tipo Durer? Para isso, usaremos o aplicativo Geogebra (ggbm.at/wvxEdpJ7). Movimente o seletor para ver a animação.

---

Fonte: bit.ly/2Huzflb

30.

a) Complete corretamente os resultados obtidos na n-ésima iteração do processo de construção do Fractal circular do tipo Dürer:

Etapas	Número de círculos	Medida do raio	Comprimento de cada círculo
$$0$$	$$1$$	$$R$$	$$2 \pi R$$
$$1$$	$$6$$	$$\frac{R}{3}$$	$$2 \pi \frac{R}{3}$$
$$2$$	$$6^{2}$$	$$\frac{R}{3^{2}}$$	$$2 \pi \frac{R}{3^{2}}$$
$$3$$	$$6^{3}$$	$$\frac{R}{3^{3}}$$	$$2 \pi \frac{R}{3^{3}}$$
...	...	...	...
$$n$$

  Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.

Etapas	Área de cada círculo	Comprimento total	Área total
$$0$$	$$2 \pi R^{2}$$	$$2 \pi R$$	$$2 \pi R^{2}$$
$$1$$	$$2 \pi \Big( \frac{R}{3} \Big)^{2}$$	$$6 \Big( 2 \pi \frac{R}{3} \Big)$$ $$= 4 \pi R$$	$$6 \Bigg( 2 \pi \Big( \frac{R}{3} \Big)^{2} \Bigg)$$ $$= \frac{2}{3} \pi R^{2}$$
$$2$$	$$2 \pi \Big( \frac{R}{3^{2}} \Big)^{2}$$	$$6^{2} \Big( 2 \pi \frac{R}{3} \Big)$$ $$= 8 \pi R$$	$$6^{2} \Bigg( 2 \pi \Big( \frac{R}{3} \Big)^{2} \Bigg)$$ $$= \frac{2^{2}}{3^{2}} \pi R^{2}$$
$$3$$	$$2 \pi \Big( \frac{R}{3^{3}} \Big)^{2}$$	$$6^{3} \Big( 2 \pi \frac{R}{3} \Big)$$ $$= 16 \pi R$$	$$6^{3} \Bigg( 2 \pi \Big( \frac{R}{3} \Big)^{2} \Bigg)$$ $$= \frac{2^{3}}{3^{3}} \pi R^{2}$$
...	...	...	...
$$n$$

  Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.

b) O comprimento e a área total do Fractal circular do tipo Dürer são, respectivamente: ∞ e .

---

31.

Observe a imagem abaixo de um fractal do tipo Dürer e desembaralhe as letras para descobrir seu nome.

Fonte: bit.ly/2rv9RBO

AEPGOFC RDIETAANNP OU DLTR OARTL

---

32.

No quadro abaixo, você identifca uma das etapas da construção de um fractal do tipo Dürer? Qual?

(a)

(b)

(c)

(d)