
Fractais e sua arte
Fractal colar de Apolônio


Fonte: bit.ly/2EX60BX
Apolônio de Perga foi um grande geômetra grego, contemporâneo de Arquimedes, que viveu, aproximadamente, entre 287 a.C. e 212 a.C. Ele propôs o seguinte problema: encontrar um círculo tangente a três outros círculos. Apolônio descobriu que existem dois círculos que não se interceptam e são tangentes aos dois círculos originais. Estes círculos são chamados apolônícos.
Considerando o problema de Apolônio como um processo iterativo podemos construir o fractal chamado colar de Apolônio.
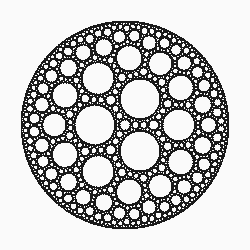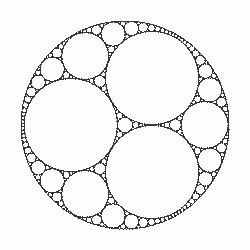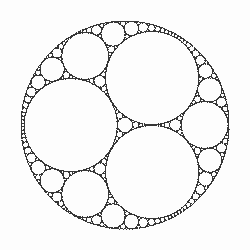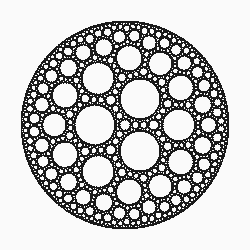
Começe com três círculos $C_{1}$, $C_{2}$ e $C_{3}$ que não se interceptam e são tangentes entre si. Se $C_{4}$ e $C_{5}$ são os círculos descobertos por Apolônio temos cinco círculos tangentes entre si.
Tomemos um dos círculos apolônícos, por exemplo $C_{4}$, sabemos que $C_{4}$ é tangente a $C_{1}$ e $C_{2}$ e logo, este trio tem dois círculos apolônícos, Sabemos que um deles é o círculo $C_{3}$, mas o outro é um novo círculo, rotulado de $C_{6}$. Agora, podemos construir um novo círculo $C_{7}$ tomando o trio $C_{4}$, $C_{2}$ e $C_{3}$ e outro $C_{8}$ tomando o trio $C_{4}$, $C_{1}$ e $C_{3}$. Deste modo, teremos três novos círculos, rotulados por $C_{6}$, $C_{7}$ e $C_{8}$.
Por outro lado, podemos construir três novos círculos tomando $C_{5}$. No final, teremos onze novos círculos (cinco existentes e seis novos). Continuando este processo indefinidamente construíremos o fractal Colar de Apolônio.
33.
Vamos desenhar algumas etapas do fractal Colar de Apolônio? Para isso, useremos o aplicativo Geogebra (ggbm.at/PWS5wuvx). Movimente o seletor para ver a animação.
Existem muitas váriações do Colar de Apolônio, veja algumas:
 Fonte: http://bit.ly/2qGXgLj |
 |
34.
Complete corretamente a tabela com os resultados obtidos na n-ésima iteração do processo de construção do fractal Colar de Apolônio:
| Etapas | Número de novos círculos | Número total de círculos novos |
| $$0$$ | $$0$$ | $$5 = 3 + 2$$ |
| $$1$$ | $$2 \cdot 3$$ | $$11 = 3^{2} + 2$$ |
| $$2$$ | $$2 \cdot 3^{2}$$ | $$29 = 3^{3} + 2$$ |
| $$3$$ | $$2 \cdot 3^{3}$$ | $$83 = 3^{4} + 2$$ |
| ... | ... | ... |
| $$n$$ |
Se estiver tendo dificuldade de preencher os espaços com as fórmulas matemáticas, clique no espaço que deseja preencher e utilize os botões abaixo para lhe auxiliar.


Em 1643, René Descartes escreveu uma carta à rainha Elizabeth de Bohemia apresentando uma fórmula para calcular os raios dos círculos do problema de Apolônio. Elizabeth, que também gostava de Matemática, apresentou uma prova alternativa da fórmula. O teorema é o seguinte:
Teorema de Descartes
Seja $r1$, $r2$ e $r3$ os raios de três círculos tais que
- $r_{1}$ é o raio do círculo $C_{1}$ externo com curvatura $k_{1} = \frac{-1}{r_{1}}$;
- $r_{2}$ e $r_{3}$ são raios dos círculos internos $C_{2}$ e $C_{3}$ ao círculo $C_{1}$ com curvaturas positivas;
- Os círculos $C_{2}$ e $C_{3}$ são tangentes à $C_{1}$ e são tangentes entre si. Não há intersecção entre os círculos.
Então, o raio $r_{4}$ do círculo $C_{4}$ que é tangente aos círculos $C_{1}$, $C_{2}$ e $C_{3}$ satisfaz a seguinte fórmula, conhecida como fórmula de Descartes:
$$\frac{1}{r_{4}} = \frac{1}{r_{1}} + \frac{1}{r_{2}} + \frac{1}{r_{3}} + 2 \sqrt{ - \frac{1}{r_{1}r_{2}} - \frac{1}{r_{1}r_{3}} + \frac{1}{r_{2}r_{3}} } $$
35.
Considere $r_{1}$, $r_{2}$ e $r_{3}$ os raios dos três primeiro círculos do Colar de Apolônio. Tomando $r_{2}=\frac{2}{3}r_{1}$ e $r_{3}=\frac{1}{3}r_{1}$ e usando a fórmula de Descartes complete a seguinte tabela:
| Círculos | Raios | |
| $$C_{1}$$ | $$r_{1}$$ | $$12$$ |
| $$C_{2}$$ | $$r_{2} = 2 \cdot \frac{r_{1}}{3}$$ | $$8$$ |
| $$C_{3}$$ | $$r_{3} = \frac{r_{1}}{3}$$ | $$4$$ |
| $$C_{1} \cap C_{2} \cap C_{3} $$ | $$r_{4} = 2 \cdot \frac{r_{1}}{7}$$ | |
| $$C_{1} \cap C_{2} \cap C_{4} $$ | $$r_{5} = \frac{r_{1}}{5}$$ | |
| $$C_{1} \cap C_{2} \cap C_{5} $$ | $$r_{6} = 2 \cdot \frac{r_{1}}{15}$$ | |
| $$C_{1} \cap C_{2} \cap C_{6} $$ | $$r_{7} = \frac{r_{1}}{11}$$ | |
| $$C_{1} \cap C_{2} \cap C_{7} $$ | $$r_{8} = 2 \cdot \frac{r_{1}}{31}$$ | |
| $$C_{1} \cap C_{2} \cap C_{8} $$ | $$r_{10} = \frac{r_{1}}{21}$$ | |
| $$C_{1} \cap C_{3} \cap C_{4} $$ | $$r_{9} = 2 \cdot \frac{r_{1}}{19}$$ | |
| $$C_{1} \cap C_{4} \cap C_{5} $$ | $$r_{12} = 2 \cdot \frac{r_{1}}{27}$$ |

Use o aplicativo Mosaico Fractal (editaedi.ufpa.br/ferramentas/mosaico) para criar um lindo Colar de Apolônio. O colar abaixo foi criado pela profa. Cristina Vaz.

36.

O historiador grego Políbio inventou um código usando a seguinte tabela com 5 linha e 5 colunas:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | A | B | C | D | E |
| 2 | F | G | H | I | J |
| 3 | K | L | M | N | O |
| 4 | P | Q | R | S | T |
| 5 | U | V | W | X | Z |
Por exemplo, a letra M corresponde ao número 33.
Inspirado em Políbio, inventei um código similar. Você saberia descodificar a mensagem com a ajuda da tabela abaixo? (coloque os devidos acentos)
| A | B | C | D | E |
| F | G | H | I | J |
| K | L | M | N | O |
| P | Q | R | S | T |
| U | V | W | X | Z |
22, 27, 37, 55, 211, 57, 77, 22, 511, 32, 75, 22, 25, 711, 22, 53, 27, 511, 25, 511, 53, 22, 75, 27, 211, 22, 72, 511, 53, 511, 57, 37, 511, 211, ...... 1.3057
